All on (Solution)

Let’s declare 6 variables:

• \(d0\) is the expected number of turns until all 6 switches are on when 0 switches are on
• \(d1\) is the expected number of turns until all 6 switches are on when 1 switch is on
• \(d2\) is the expected number of turns until all 6 switches are on when 2 switches are on
• \(d3\) is the expected number of turns until all 6 switches are on when 3 switches are on
• \(d4\) is the expected number of turns until all 6 switches are on when 4 switches are on
• \(d5\) is the expected number of turns until all 6 switches are on when 5 switches are on

We can then construct the following system of equations:

\[\begin{align*} d0 &= 1 + d1 \\ d1 &= 1 + 1/6 \cdot d0 + 5/6 \cdot d2 \\ d2 &= 1 + 2/6 \cdot d1 + 4/6 \cdot d3 \\ d3 &= 1 + 3/6 \cdot d2 + 3/6 \cdot d4 \\ d4 &= 1 + 4/6 \cdot d3 + 2/6 \cdot d5 \\ d5 &= 1 + 5/6 \cdot d4 + 1/6 \cdot 0 \\ \end{align*}\]

Since I’m lazy, I just asked python to solve them for me:

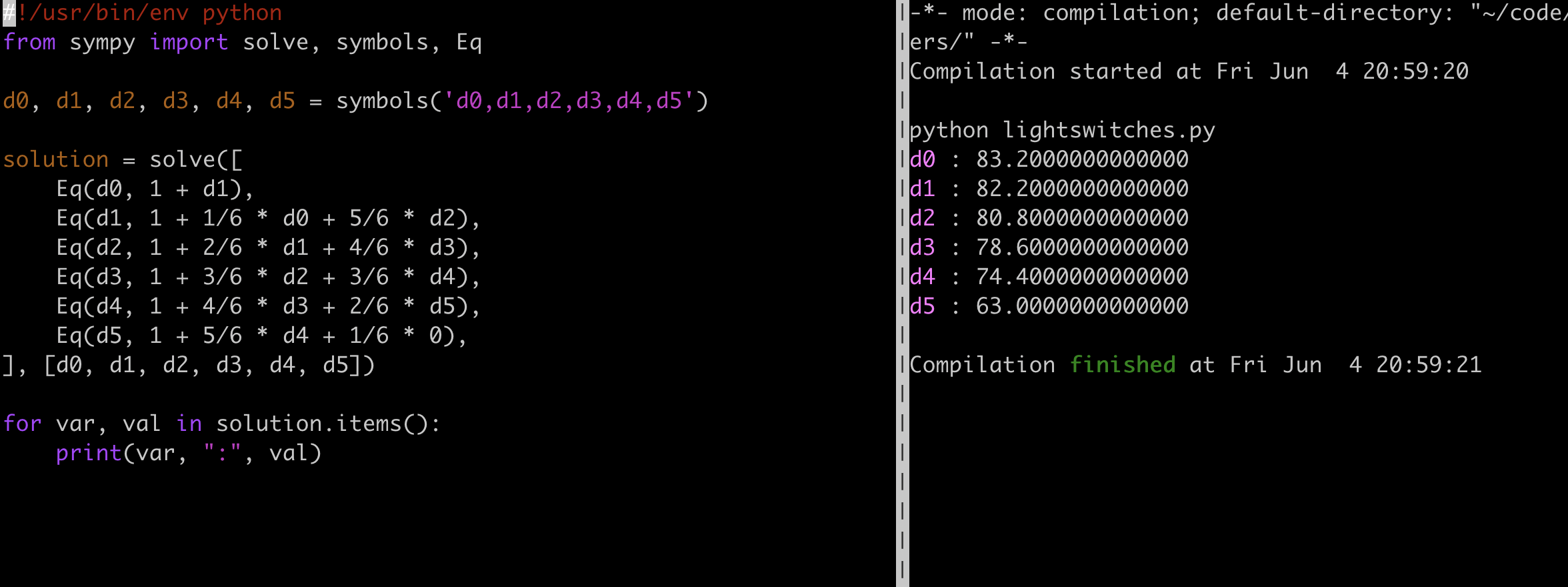
The answer we are looking for is \(d0\) which is 83.2.